Varför är stora båtar slankare än små
Stabiliteten är kanske den viktigaste egenskapen hos en segelbåt. Tillräcklig stabilitet är en förutsättning för att båten skall vara säker att segla. En mer stabil båt kan bära mer segel vilket ger större drivkraft. Men hur uppkommer stabiliteten? Hur påverkas den av skrovets form? Hur viktig är båtens tyngd och tyngdpunkt? Frågorna är många. Lars Larsson, Professor i Hydrodynamik vid Chalmers, har svaren.
Det här är fjärde artikeln i serien om teorierna bakom design och konstruktion av segelbåtar. Tidigare har vi bekantat oss med båtens motstånd i vattnet (#1 och #2 2015) och diskuterat optimering av en segelbåts akterskepp (#3 2015). I den här artikeln tittar vi närmare på en ännu viktigare aspekt inom området båtkonstruktion: stabiliteten. Vi avslutar med att besvara frågan: Varför är stora båtar slankare än små?
För en segelbåt med konstant hastighet på rak kurs är alla krafter och moment balanserade. Krängande momentet från seglen är i exakt balans med rätande momentet från skrov och köl. Vi kommer snart att se hur det rätande momentet skapas när båten kränger, och hur viktfördelningen och skrovets form bestämmer stabiliteten. Men vi börjar med att repetera det grundläggande begreppet flytkraft som kort förklarades i #2.
Flytkraft
Vi har tidigare delat upp vattentrycket i två komponenter: det hydrostatiska och det hydrodynamiska. Det hydrostatiska trycket beror endast av vattnets tyngd. Varje liten kub vatten bär vikten av den vattenpelare som står på dess översida. Det hydrostatiska trycket är därmed proportionellt mot djupet under vattenytan (eller höjden av vattenpelaren). Det hydrostatiska trycket kan bara mätas i stillastående vatten. För vatten i rörelse avviker trycket från det hydrostatiska. Avvikelsen är det hydrodynamiska trycket.
Flytkraft och stabilitet bestäms i praktiken alltid när båten ligger stilla. Vattnet rör sig inte, och det är bara det hydrostatiska trycket som spelar någon roll. Figur 1 visar hur flytkraften uppstår. För enkelhetens skull har vi valt att visa en lådformad kropp istället för en segelbåt. De vertikala pilarna i figuren representerar det hydrostatiska trycket som verkar på lådans botten och skapar en kraft uppåt: flytkraften. De horisontella tryckkrafterna på lådans sidor bidrar inte. För en båt (som flyter) är flytkraften exakt lika stor som båtens tyngd.
Flytkraften verkar i undervattenskroppens flytcentrum (B). För lådan i figuren ligger det på halva djupgåendet. Tyngden verkar i lådans tyngdpunkt (G). I figuren har vi antagit att den ligger på vattenlinjen. Lådan anpassar djupgåendet så att de två krafterna är i jämvikt.
Stabilitet
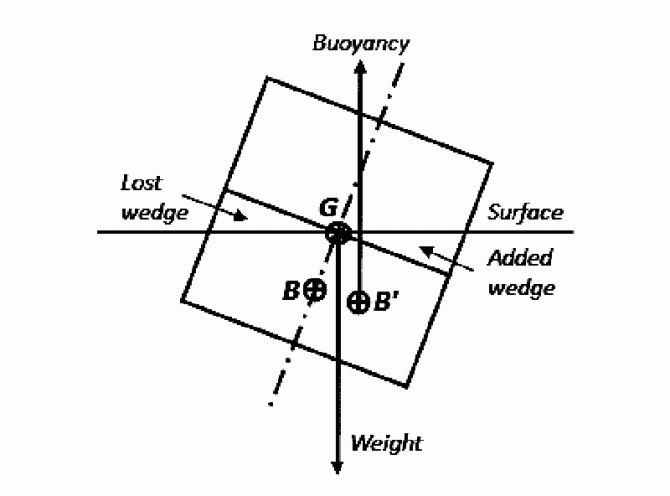
När en segelbåt kränger ökar den nedsänkta volymen kilformat på läsidan samtidigt som den minskar på samma sätt i lovart. Detta demonstreras i Figur 2 och för enkelhetens skull använder vi återigen den lådformade kroppen. Observera att den ökade volymen måste vara exakt lika stor som den minskade för att flytkraften skall vara i jämvikt med tyngdkraften. Kilarna måste ha exakt samma volym. Lådan åstadkommer detta genom att rotera kring sin egen centrumlinje. I fallet med en segelbåt, med icke-vertikala sidor, lyfts skrovet något när båten kränger. På grund av den ökade volymen i lä och den minskade volymen i lovart kommer den krängda volymens flytcentrum (B’) att förflyttas från B i riktning mot läsidan. Ett moment skapas mellan flytkraft och tyngdkraft. Detta är det rätande momentet.

Figur 3 visar en mer komplett bild av en segelbåt. Vi känner igen punkterna B, B’ och G, men vi ser också några fler definitioner. GZ är avståndet mellan tyngd- och flytkraft, det vill säga den rätande hävarmen, och GM är avståndet mellan tyngdpunkten och punkten M, kallad ”metacentrum”. M ligger där en vertikal linje genom B’ skär båtens symmetriplan. För små krängningsvinklar (upp till 10 grader) är punkten så gott som fixerad. Oavsett krängningen verkar flytkraften längs en linje genom samma punkt. Detta gäller dock inte för större krängningsvinklar.

Figur 3. En segelbåt i jämvikt. Grundläggande begrepp.
Hävarmskurvan
Figur 4 visar hävarmskurvan (GZ-kurvan) för krängningsvinklar mellan 0 och 180 grader. Multiplicerar man GZ på den vertikala axeln med båtens tyngd fås det rätande momentet. Kurvan i figuren gäller för en modern performance cruiser på 41 fot med bulbköl. Med jämna mellanrum visas ett tvärsnitt av segelbåten med tyngd- och flytkraft utritade som pilar.
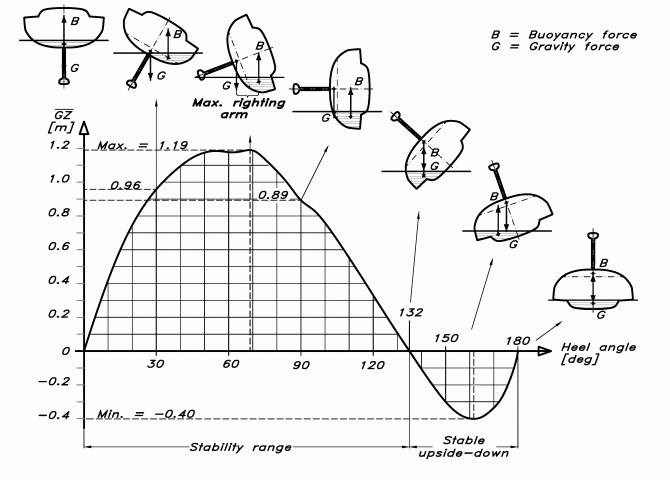
Figur 4. Hävarmskurvan. Den rätande hävarmen för en modern 41 fots performance cruiser vid olika krängningsvinklar.
Vid 0 graders krängning verkar krafterna längs samma linje i centerplanet (på samma sätt som i Figur 1). GZ är 0 liksom momentet. Vid 30 grader är de två krafterna väl separerade och GZ är 0,96 m. Det längsta avståndet mellan krafterna (GZ = 1,19 m) inträffar vid 69 grader. Vid större krängningsvinklar närmar sig de båda krafterna varandra igen. Vid 90 grader kan vi se en knyck på kurvan. Det är där ruffsidan träffar vattenytan. Kurvan går genom 0 vid 132 grader. Denna vinkel kallas “angle of vanishing stability” och bestämmer båtens stabilitetsvidd (se Figur 4). Här verkar de två krafterna igen längs samma linje. För större vinklar blir avståndet mellan krafterna negativt (GZ < 0). Flytkraften ligger till vänster om tyngdkraften och tillsammans tenderar de att öka krängningen, det vill säga vrida båten till ett stabilt läge vid 180 grader. Det maximala krängande momentet inträffar vid 162 grader där GZ är -0,40 meter.
De viktigaste parametrarna hos GZ-kurvan är dess lutning vid mindre krängningsvinklar, det högsta värdet, stabilitetsvidden och arean ovanför respektive nedanför den horisontella axeln. Kurvans lutning vid små vinklar bestämmer krängningsvinkeln vid normala seglingsförhållanden. Övriga parametrar är viktiga vid mer extrema förhållanden. Det högsta värdet på GZ avgör gränsen för en båts segelarea eftersom rätande momentet vid denna vinkel är det största möjliga. Om krängande momentet från seglen överskrider detta värde kapsejsar segelbåten. Stabilitetsvidden och speciellt arean under kurvan fram till nollgenomgången är viktiga för segelbåtens dynamiska egenskaper. Om båten träffas av en kraftig vindby eller en stor våg kommer den i rullning och den överförda energin absorberas genom att krängningsvinkeln ökar. Om arean under kurvan är tillräckligt stor absorberas all överförd energi innan kapsejsning och båten återvänder till en mer upprätt position. Om inte, kommer båten att kapsejsa.

Anledningen till att arean nedanför den horisontella axeln är viktig är att den representerar den energi som krävs för att vända båten tillbaka till upprätt läge när den väl ligger upp och ner. Om arean är stor krävs en mycket stor våg för att vända båten rätt. För de flesta segelbåtar är dock den här arean så liten att de vågor som träffar skrovet räcker till för att puffa båten rätt.
Skrovform och vikt
Låt oss återgå till Figur 3 och identifiera de parametrar som bestämmer stabiliteten vid normala krängningsvinklar. Rätande momentet fås genom att multiplicera den rätande hävarmen, GZ, med tyngdkraften. För en given krängningsvinkel är GZ proportionell mot GM, kallad ”metacenterhöjden”.
Frågan är då vad som bestämmer GM, avståndet mellan G och M, som bör vara så stort som möjligt för att skapa god stabilitet. Uppenbarligen beror G på båtens viktfördelning. Stor tyngd långt ner sänker G. Ett bra exempel på detta är bulbkölen som sänker tyngdpunkten avsevärt. Ett annat sätt att sänka G är att minska vikten högt upp. Kolfibermaster är avsevärt lättare än aluminiummaster vilket innebär att G kan sänkas en hel del genom att byta ut aluminiummasten mot en kolfibermast.
För att höja M måste B’ förflyttas åt lä. Detta kan man åstadkomma genom en bredare båt. Faktum är att stabiliteten är väldigt beroende av båtens bredd.
Segelbåtar med låg tyngdpunkt sägs vara ”viktstabila”. Exempel på detta är R-båtar som är smala och har den mesta vikten koncentrerad i den stora blykölen. Mer moderna segelbåtar, speciellt av fransk design, är väldigt breda och lätta. De är ”formstabila” och har metacentrum högt upp.
Efter katastrofen i Fastnet Race 1979 jämförde Southamptons Universitet stabiliteten hos två segelbåtar av liknande storlek och med praktiskt taget samma segelyta och GM. Den ena var den traditionella långkölade Contessa 32 och den andra, den lätta och fenkölade 30-fotaren “Grimalkin”. Figur 5 visar GZ-kurvan för dessa båda båtar.

Figur 5. En jämförelse mellan GZ-kurvorna för den långkölade Contessa 32 och den lätta, fenkölade kappseglaren Grimalkin.
Inom området för normala krängningsvinklar, upp till 20 grader, ser kurvorna nästan identiska ut. Detta beror på att GM är detsamma. Då båtarnas vikt skiljer sig (Contessa 32 ligger på 4600 kg och Grimalkin på 3800 kg) är stabiliteten högre för den mer traditionella båten som därmed kränger mindre under normala seglingsförhållanden.
Den riktigt viktiga skillnaden återfinns dock vid större krängningsvinklar. Grimalkin når sitt största värde på GZ vid 50 grader medan Contessa når sitt maximum vid 80 grader, och där är GZ 40% högre. Räknar man om det till båtarnas största rätande moment skiljer det hela 70%. Stabilitetsvidden är 115 grader för den fenkölade segelbåten, och 155 grader för den långkölade. Vi kan också se att det är stora skillnader i areorna under respektive GZ-kurva. Contessa har en stor area över, och en liten area under den horisontella axeln, medan Grimalkin har en positiv area som är mycket mindre än Contessas, samtidigt som den har en avsevärd area med negativ rätande hävarm. Areorna visar att Grimalkin har mycket lättare att kapsejsa och mycket mindre chans att återhämta sig jämfört med Contessa.
Den här undersökningen genomfördes för över 35 år sedan. Resultatet pekade på riskerna med breda och lätta skrov. Sedan dess har tyngdpunkten sänkts, dels på grund av bulbkölen, dels på grund av att alla båtar till salu inom EU måste delas in i olika kategorier beroende på deras sjövärdighet. Areorna ovan och under den horisontella axeln på GZ-kurvan är viktiga parametrar i den klassificeringen.
Uppskalning av stabiliteten
Låt oss nu svara på frågan i artikelrubriken: ”Varför är stora båtar slankare än små?” Säg att vi skalar upp en båt likformigt. Alla längdmått hos båten ökas då med samma procentsats; de är proportionella mot båtens längd, L. Ytmåtten skalas som längden i kvadrat, L2 och volymmåtten som längden i kubik, L3.
Rätande hävarmen GZ är en längd och skalas som L. För att få rätande momentet multipliceras GZ med båtens tyngd, som är proportionell mot undervattensvolymen. Denna skalas som L3. Totalt skalas alltså rätande momentet som L4.
Krängande momentet är proportionellt mot segelarean gånger avståndet mellan segelcentrum och tryckcentrum på undervattenskroppen. Detta avstånd skalas med L för geometriskt likformiga segelbåtar. Då segelarean skalas som L2 skalas krängande momentet som L3.
När båten skalas upp likformigt ökar alltså rätande momentet snabbare än krängande momentet. Om vi till exempel dubblerar storleken på en segelbåt kommer rätande momentet att öka 24 = 16 gånger medan krängande momentet ökar 23 = 8 gånger. Den stora segelbåten kommer vara onödigt styv. Detta innebär att när man skalar upp en båt bör inte bredden öka i samma takt som längden, skrovet blir slankare.
I diskussionen ovan har vi inte tagit hänsyn till att vindhastigheten ökar med höjden över havet. Dessutom ökar normalt inte kölens djupgående i proportion till skrovlängden, vilket vi antagit. Dock är dessa effekter ganska små, så resonemanget gäller i huvudsak; en stor båt är i regel slankare än en liten.
Lär dig mer
Vill du lära dig mer kan du skaffa boken ”Principles of Yacht Design” (Fjärde upplagan, 2014) av Lars Larsson, Rolf E Eliasson och Michal Orych. En kurs baserad på boken kommer att hållas i Stockholm och Göteborg vintern 2016. Besök www.isyd.org för mer information.
Text Professor Lars Larsson
Foto Search Magazine
Vi tackar förlaget Adlard Coles Nautical, London, för möjligheten att publicera Figurerna 3, 4 och 5 som är tagna ur boken Principles of Yacht Design.
Lars Larsson artiklar om teorierna bakom design och konstruktion av segelbåtar:
#1 Skrovlig eller slät yta – spelar det någon roll?
#2 Varför är en lång båt snabbare än en kort?
#3 Brett och platt akterskepp – ett lyckat koncept – eller inte?
#4 Varför är stora båtar slankare än små?
#5 Snabb eller långsam? Hur bedömer man en segelbåts prestanda?



































