Design av köl och roder
DESIGN AV KÖL OCH RODER
Vad kan vi lära av flygplanskonstruktörer? Hur kan ett plan flyga? Vad är en elliptisk kraftfördelning? Varför är en djup och smal köl bättre än en grund och bred? Hur ser det optimala rodret ut? Hur stor betydelse har kölbulben på en modern segelbåt? Frågorna är många. Lars Larsson, Professor i Hydrodynamik vid Chalmers, har svaren.
På en kryssbog är seglens drivkraft avsevärt mindre än den oönskade sidkraften. Denna leder till krängning och avdrift, två fenomen som båda påverkar båtens prestanda negativt. För en båt i jämvikt måste seglens sidkraft balanseras av en lika stor kraft i motsatt riktning från segelbåtens undervattenskropp, huvudsakligen köl och roder. Därmed har vi tre vingar som bestämmer båtens prestanda på kryssen; segel, köl och roder. En optimering av dessa tre vingar är absolut nödvändig när man designar en segelbåt.
LYFTKRAFT
Den mest fundamentala frågan inom vingteorin är hur lyftkraft genereras. Varför flyger ett flygplan? En vanlig missuppfattning är att lyftkraften genereras på grund av att vägen som luften passerar är längre på vingens ovansida än på dess undersida. Den förklaringen är felaktig. Glädjande nog finns det en mycket enklare förklaring som dessutom är rätt. Den luftströmning som träffar en flygplansvinge avlänkas nedåt (Figur 1). Vingen utövar en kraft på luften som därmed tvingas ändra riktning samtidigt som luften utövar en exakt lika stor motriktad kraft på vingen. Den vertikala, uppåtriktade kraftkomponenten är lyftkraften. Denna är alltid i rät vinkel mot anströmningshastigheten. Tyvärr uppstår även en motståndskraft som är parallell med anströmningshastigheten. Summerar man de båda krafterna får man en resulterande kraft som verkar uppåt och snett bakåt (Figur 1).
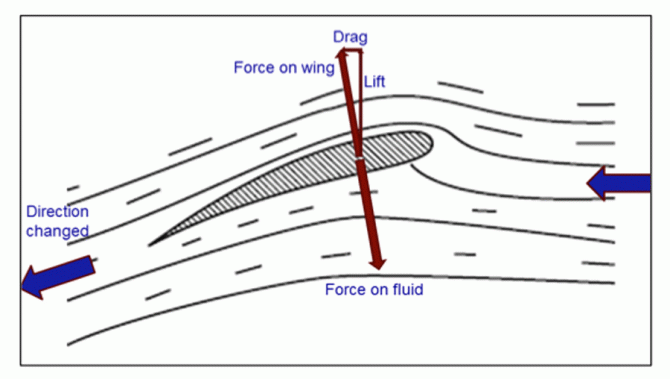
Figur 1. Vingen trycker ner luften så att den ändrar riktning. Luften trycker emot med samma kraft i motsatt riktning.
Lyftkraft kan mycket väl genereras utan anfallsvinkel om vingen är asymmetrisk. Anledningen är dock densamma; hastigheten som lämnar vingen är riktad snett nedåt på grund av vingens asymmetri.
TRYCKFÖRDELNINGN KRING EN VINGSEKTION
Figur 2 visar tryckfördelningen kring en vingsektion. Pilar som pekar utåt från vingen indikerar sug (negativt tryck) och pilar som pekar inåt indikerar positivt tryck. Det är tydligt att det sug som skapas genom det kraftigt krökta strömningen på vingens ovansida är mycket större än trycket under vingen. Den nedre delen av Figur 2 visar tryckfördelningen i diagramform. Den horisontella axeln utgör vingens bredd medan den vertikala axeln visar trycket. Det kan tyckas märkligt att negativt tryck visas uppåt i figuren men det är det vedertagna sättet att avbilda tryckfördelningen kring en vinge, som alltså har negativt tryck på ovansidan. Det är skillnaden i tryck mellan vingens undre och övre sida som ger lyftkraften.
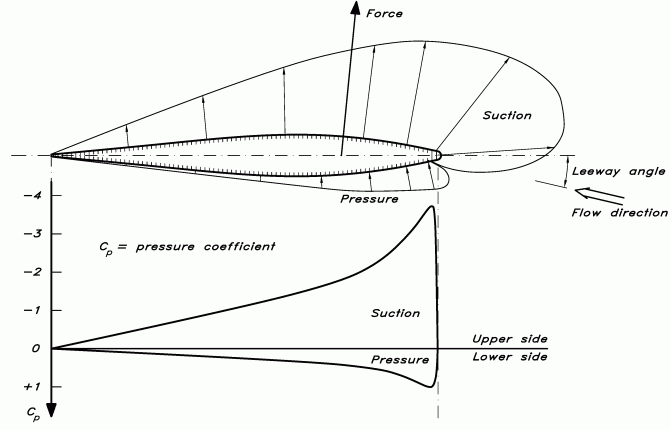
Figur 2. Tryckfördelning kring en vingsektion.
TREDIMENSIONELLA VINGAR
När en vingsektion testas i en vindtunnel används en vinge med konstant tvärsnitt som spänner över hela tunnelns bredd. Båda ändar är fästa i tunnelväggen. Fallet kallas tvådimensionellt då strömningen är densamma vid samtliga sektioner (bortsett från små områden nära tunnelns vägg). Det finns ingen variation längs vingen.
I praktiken har de flesta vingar åtminstone en fri ände. Det gäller för en flygplansvinge och det gäller för en köl och ett roder på en segelbåt. Strömningen påverkas då avsevärt av den fria änden. Figur 3 visar en köl som är fäst vid en platt botten och några strömlinjer som visar strömningsriktningen. I det här fallet är vingen vertikal och lyftkraften är riktad i sidled.
Då det råder ett högt tryck på läsidan av kölen (som motsvarar den undre sidan på en flygplansvinge) och ett lågt tryck på lovartsidan, tenderar strömningen att smita under kölens spets, från lä till lovart. Den här effekten är inte märkbar vid kölens infästning, nära skrovet, men ju djupare man kommer på läsidan desto starkare blir den nedåtgående strömningskomponenten. Vid lovartsidan är hastigheten riktad snett uppåt nere vid spetsen, men blir mer och mer horisontell när man närmar sig skrovet.
När dessa båda strömningar möts vid kölens bakkant har de olika riktningar (snett nedåt, respektive snett uppåt)och det bildas ett skikt av virvlar mellan dem. Detta skikt bildar ganska omgående en enda virvel vilket illustreras till väsnter i Figur 3 (a och b). Denna ändvirvel kan man se bakom en båt som seglar med stor krängningsvinkel. Kölens spets är då nära vattenytan och virveln, som har väldigt lågt tryck, suger luft från ytan och bildar ett långt luftrör efter båten.
Ändvirveln innehåller energi som lämnas efter båten. För att generera denna energi krävs en kraft, en motståndskomponent, som kallas inducerat motstånd. Detta måste adderas till det viskösa motståndet och vågmotståndet som förklarades i seriens andra artikel (#2 2015). Med hjälp av aerodynamisk teori kan man visa att det minsta möjliga inducerade motståndet fås när fördelningen av lyftkraften längs vingens spännvidd är elliptisk. Sidkraften på en köl är störst nära skrovet, men avtar gradvis närmare spetsen. Teorin säger alltså att avtagandet skall ske så som visas till höger i Figur 3 (c och d), där kraftkurvan har en elliptisk form.
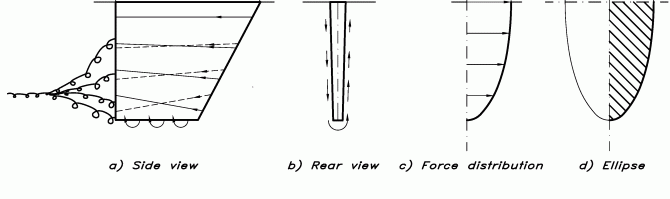
Figur 3. Strömning kring en köl. Streckade linjer; lä, heldragna linjer; lovart (a och b). Elliptisk kraftfördelning i djupled (c och d).
En elliptisk kraftfördelning fås om kölen har en elliptisk form, vilket illustreras längst till höger i Figur 3 (d). Formen är fullt möjlig för ett centerbord eller ett roder, men knappast för en köl, då volymen nära spetsen är för liten. Tyngdpunkten kommer att ligga alldeles för högt för att ge god stabilitet.
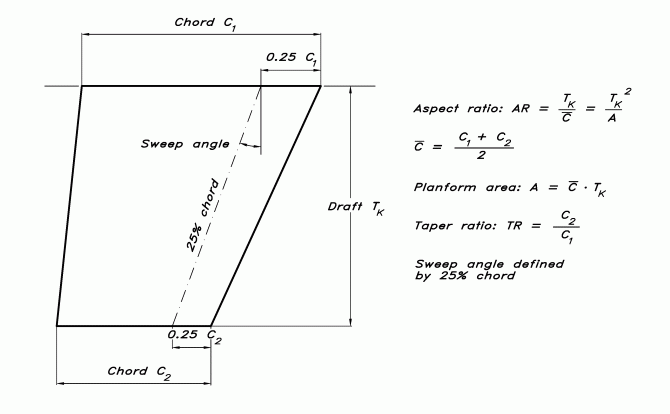
Figur 4. Definition av kölparametrar.
De flesta kölar är trapetsformade, d v s de har fyra raka sidor, vilket visas i Figur 4. Formen karaktäriseras av tre parametrar; sidoförhållandet (aspect ratio), trapetsförhållandet (taper ratio) och svepvinkeln (sweep angle). De tre parametrarna är definierade i figuren. En korda är ett horisontellt mått på kölen. Rotkordan kallas C1 och spetskordan C2 i figuren. Sidoförhållandet är djupgåendet dividerat med medelkordan. Trapetsförhållandet är spetskordan dividerat med rotkordan. Svepvinkeln definieras med hjälp av en linje som förbinder de två punkter på kölens respektive ändar som ligger 25% av kordalängden från kölens framkant. Anledningen till detta är att lyftkraften angriper på 25% av kordalängden från framkanten.
Den viktigaste parametern är sidoförhållandet. Figur 5 visar lyftkraften och motståndet på fyra vingar med olika sidoförhållanden; 1, 2, 3 och oändligheten. Det sistnämnda motsvarar det tvådimensionella fallet där vingens båda ändar är fästa i en vägg. Sidoförhållandet har en stor inverkan på lyftkraften. Upp till överstegring (där kurvorna vänder nedåt) är lyftkraften 50% större för en vinge med sidoförhållandet 2 jämfört med 1, dubbelt så stor för sidoförhållandet 3 och fyra gånger så stor för det tvådimensionella fallet.
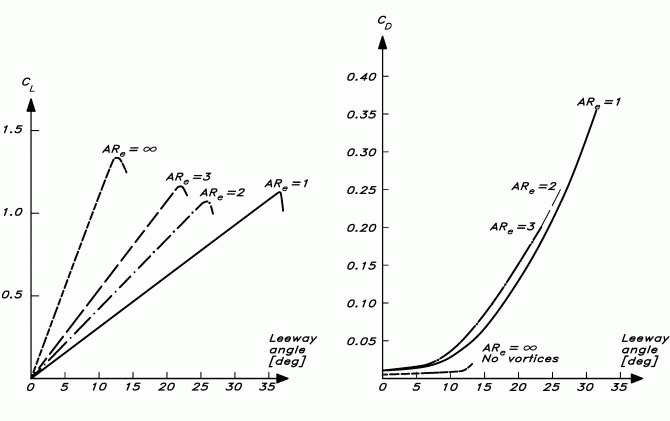
Figur 5. Sidofållandets inverkan på lyftkraften. CL och CD är lyft- och motståndkoefficienter och ARe är det effektiva sidoförhållandet.
Notera att det sidoförhållande som avses i figuren är det effektiva, som är större än det geometriska. Strömningen kring en vinge som är fäst vid en vägg med bara en fri ände skiljer sig naturligtvis från strömningen kring en vinge som har båda ändarna fria. I det senare fallet skapas två ändvirvlar istället för en. Det här tar man hänsyn till genom det effektiva sidoförhållandet. Man kan visa att det effektiva sidoförhållandet är dubbelt så stort som det geometriska för en vinge som är fäst vid en plan vägg. Detta är en god approximation även för kölar och roder som är fästa vid skrovets botten. En typisk fenköl har ett geometriskt sidoförhållande kring 1 (medelkordan är lika stor som djupgåendet) vilket innebär att det effektiva sidoförhållandet ligger kring 2. Djupgåendet för ett roder är ofta ungefär som för kölen medan dess medelkorda är mycket mindre, vilket ger ett geometriskt sidoförhållande kring 3 och ett effektivt kring 6.
Den sidkraft som krävs av en segelbåts undervattenskropp bestäms av sidkraften från seglen. De två motriktade krafterna måste vara i balans. Diagrammet i Figur 5 bör därmed läsas på omvänt sätt. Lyftkraften (som är riktad i sidled) är given och avdriften kan bestämmas. Ju större sidoförhållande desto mindre avdrift. Det här bör hållas i åtanke när man betraktar motståndet till höger i Figur 5. Det kan verka som om sidoförhållandet har liten betydelse, men så är inte fallet. Ett större sidoförhållande ger en mindre avdrift och därmed ett mindre motstånd.
De två andra parametrarna i Figur 2 har mycket mindre inverkan på det inducerade motståndet. Det finns dock ett optimalt förhållande mellan de två. Kom ihåg att den ideala fördelningen av lyftkraften är elliptiskt formad. Detta är inte möjligt att åstadkomma med en trapetsköl men nackdelen är väldigt liten om trapetsförhållandet förhåller sig till svepvinkeln som visas i Figur 6. Till exempel, om svepvinkeln är noll bör trapetsförhållandet vara 0,43. De flesta kölar är svepta bakåt åtminstone 20 grader vilket ger ett optimalt trapetsförhållande på 0,20. Det finns dock inga kölar som ser ut på det sättet. Skälet är att tyngdpunkten skulle hamna för högt vilket i sin tur skulle ge en väldigt vek båt. Som kompromiss mellan stabilitet och lågt inducerat motståndet hamnar trapetsförhållandet ofta kring 0,5 vilket innebär att det inducerade motståndet är någon procent högre än optimalt. Då man inte behöver bekymra sig om stabiliteten när det gäller roder bör de designas enligt Figur 6 om de har trapetsform.
Rodret behöver dock inte vara trapetsformat. De kan mycket väl ha en elliptisk form. Detta innebär inte nödvändigtvis att de ser ut som rodret längst till vänster i Figur 7. De två rodren till höger har också en elliptisk form men kordan är flyttad bakåt i mittenfiguren och framåt i figuren längst till höger. Av de tre rodren är det mittersta bäst. Detta beror på en liten ändeffekt som inte är inkluderad i den generella aerodynamiska teorin som vi hänvisat till tidigare. Generellt är det fördelaktigt att rodrets (och kölens) djupaste punkt ligger vid bakkanten.
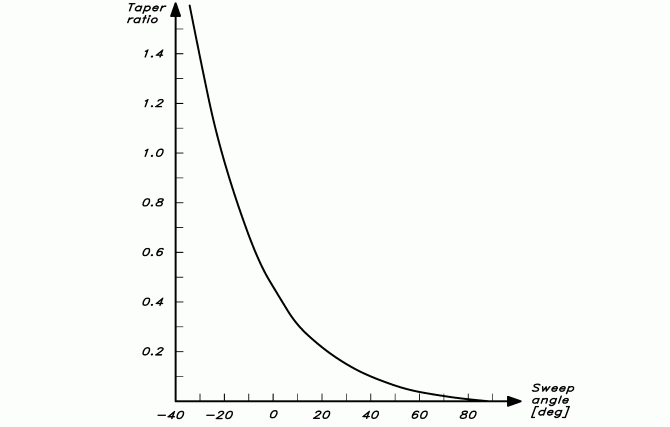
Figur 6. Optimal relation mellan svepvinkel och trapetsförhållande. Positiv vinkel akteröver.
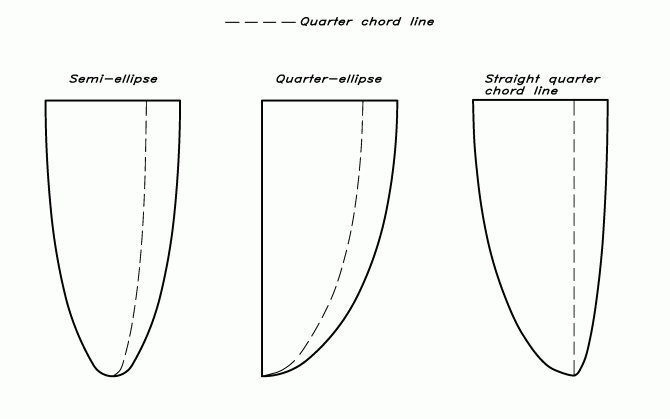
Figur 7. Exempel på former med en elliptisk kordafördelning.
BULBKÖLAR
Rena fenkölar används sällan på moderna segelbåtar. Av stabilitetsskäl finns det nästan alltid någon form av bulb. I ett forskningsprojekt vid Chalmers undersöktes fyra kölar; en ren fenköl och tre bulbkölar. Samtliga visas i Figur 8. Den integrerade bulbkölen har en mjuk övergång mellan bladet och bulben, medan T-kölarna har en mer distinkt bulb.
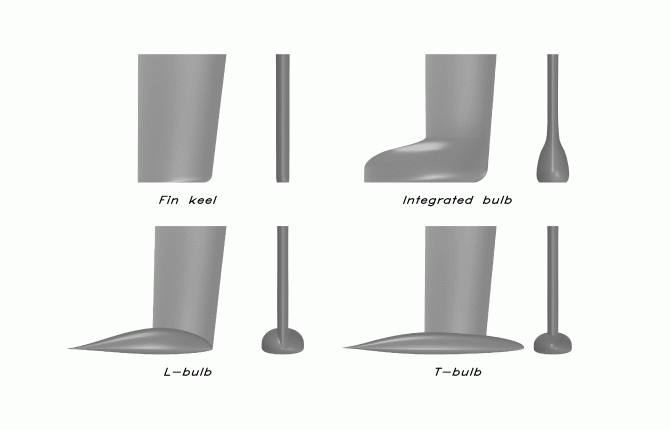
Figur 8. De fyra kölar som undersöktes på Chalmers.
Samtliga bulbkölar hade samma rätande moment medan fenkölens rätande moment var mycket mindre. Undersökningen gjordes dels i vindtunnel, dels med hjälp av numerisk strömningsberäkning (CFD). VPP-beräkningar (som diskuterades i #5 2015) omvandlade sedan skillnaderna till sekunder per sjömil. Resultaten presenteras i Tabell 1.
Tabell 1. Sekunder per sjömil för de fyra olika kölarna.
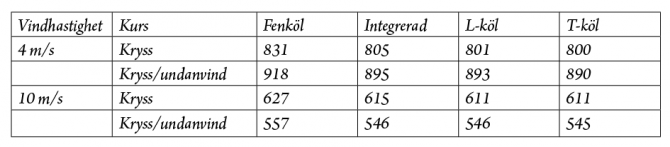
Tabellen visar resultaten för ren kryss och en blandad kurs bestående av 50% kryss och 50% undanvindssegling vid två vindhastigheter; 4 och 10 m/s. Då stabiliteten skilde sig mycket mellan fenkölen och de övriga kölarna justerades segelarean så att samtliga kölar seglade med samma krängningsvinkel (Dellenbaughvinkel som behandlades i #4 2015). Man tog även hänsyn till effekter från olika dimensioner på mast och rigg p g a de olika segelytorna. Det är tydligt att fenkölen är underlägsen de tre bulbkölarna i samtliga fall. Skillnaden mellan bulbkölarna är liten, men man kan ändå dra slutsatsen att det bästa valet är T-kölen.
Det här är den sjätte artikeln i serien om teorierna bakom design och konstruktion av segelbåtar. Tidigare har vi bekantat oss med båtens motstånd i vattnet (#1 och #2 2015) och diskuterat optimering av en segelbåts akterskepp (#3 2015). I den fjärde artikeln tittade vi närmare på en segelbåts stabilitet (#4 2015) och i den femte artikeln hur man bedömer en segelbåts prestanda (#5 2015).
Vill du lära dig mer kan du skaffa boken ”Principles of Yacht Design” (Fjärde upplagan, 2014) av Lars Larsson, Rolf E Eliasson och Michal Orych. En kurs baserad på boken kommer att hållas i Stockholm och Göteborg februari-mars 2016. Besök www.isyd.org för mer information.
Text Professor Lars Larsson
Foto Search Magazine
Vi tackar förlaget Adlard Coles Nautical, London, för möjligheten att publicera Figurerna 2-9, som är tagna ur boken ”Principles of Yacht Design”.
Lars Larsson artiklar om teorierna bakom design och konstruktion av segelbåtar:
#1 Skrovlig eller slät yta – spelar det någon roll?
#2 Varför är en lång båt snabbare än en kort?
#3 Brett och platt akterskepp – ett lyckat koncept – eller inte?
#4 Varför är stora båtar slankare än små?
#5 Snabb eller långsam? Hur bedömer man en segelbåts prestanda?




































